VAE学习笔记

参考

我的学习资料：

ML Lecture 18: Unsupervised Learning - Deep Generative Model (Part II) - YouTube

From Autoencoder to Beta-VAE | Lil’Log

[1312.6114] Auto-Encoding Variational Bayes

我的学习笔记中引用的截图出处都在上面的资料里。

笔记

概念与名词

先回顾一下 auto-encoder。auto-encoder 是一个以无监督的方式自学压缩和还原数据的神经网络结构，用于从数据中学习其本质特征，发掘更高效的压缩表示。

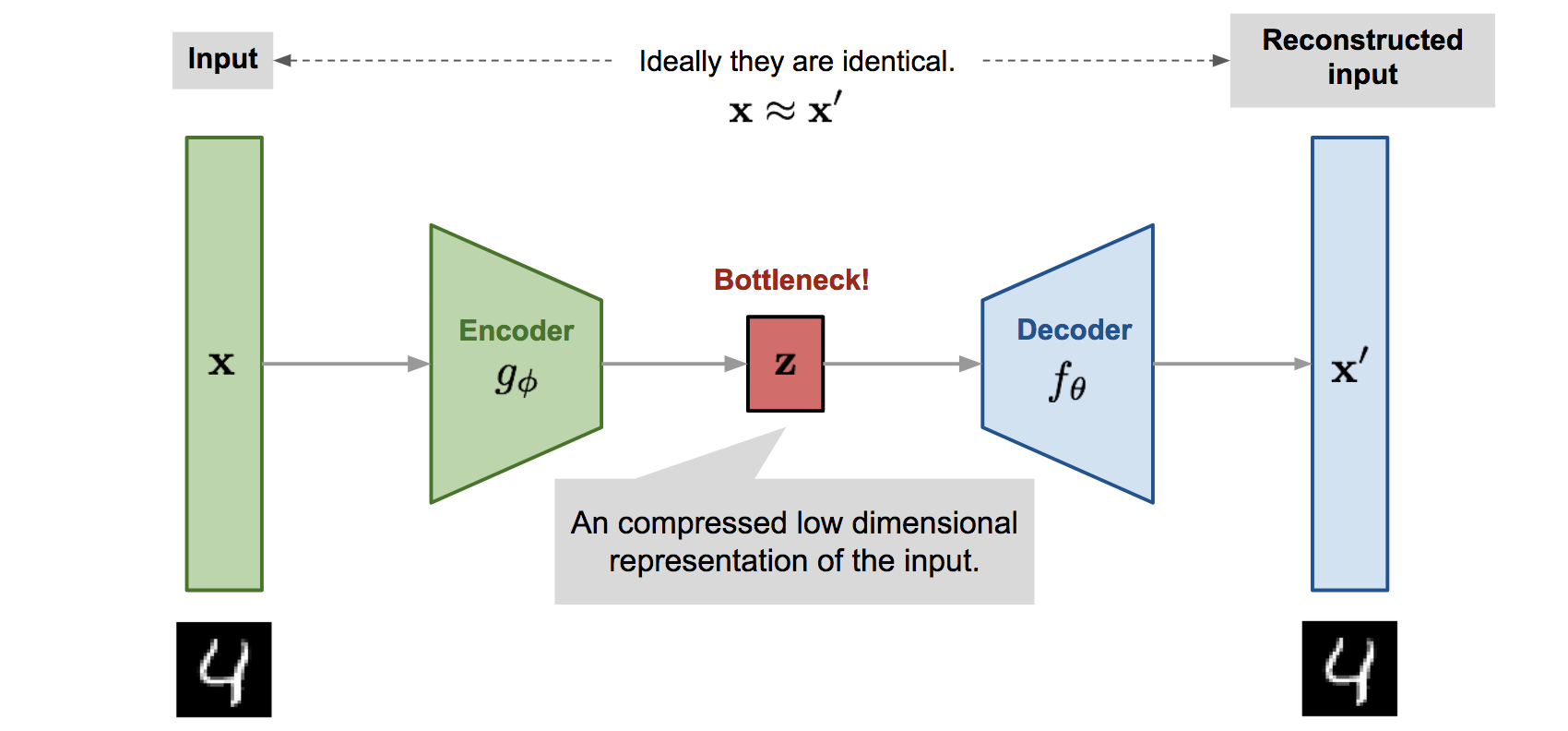
它的 encoder 学会编码数据，就是将原始的高维输入样本$x$转换为低维潜在变量（latent variable）$z$。一般表示为$g_\phi(·)$。

它的 decoder 学会从编码中还原数据，就是将$z$还原为重构（reconstructed ）向量$x’$。一般表示为$f_\theta(·)$。

因此，上述概念可以表示为

$$z=g_\phi(·)$$ $$x'=f_\theta(g_\phi(x))$$

目标是训练 $\theta$和$\phi$，使得

$$x\approx f_\theta(g_\phi(x))$$

loss 函数有一些选择，可以用交叉熵、MSE 等，用 MSE 就是：

$$L_{\text{AE}}(\theta, \phi) = \frac{1}{n} \sum_{i=1}^{n} \left(\mathbf{x}^{(i)} - f_\theta(g_\phi(\mathbf{x}^{(i)}))\right)^2$$

概率论补充：

一个概率分布（比如 P(A) 或者 P(A∣B)）是用来描述某个事件发生的可能性的。

• 如果是离散的，它会列出每个可能值及其对应的概率。

• 如果是连续的，它会用一个概率密度函数来描述，曲线下的面积代表概率。

• 例如，如果 $p_θ(z)=\mathcal N(0,I)$，那么它就是一个正态分布的概率密度函数。

  $pθ(z=z_{具体值})$告诉你某个具体 z 值出现的概率密度是多少，而不是直接的概率。要得到概率，你需要在 z 的某个小区间上进行积分。

VAE（变分自编码器，Variational Auto-encoder）并不准备像刚才那样将输入映射到固定的变量，而是要把输入映射到分布。这个分布记为$p_\theta$。输入$x$与潜在编码向量$z$有这样的关系：

• $p_\theta(z)$是先验（prior），它代表潜在编码向量 z 的先验分布，指的是我们在没有看到任何真实数据 x 的情况下，对潜在空间 Z 中任何一个潜在向量 z 的先验预设分布。
  在 VAE 中，我们常常设定为：

  $$p_\theta(\mathbf{z}) = \mathcal{N}(\mathbf{0}, \mathbf{I})$$

• $p_\theta(x \mid z)$是似然（likelihood），它代表给定潜在编码向量 z 的情况下，生成原始数据 x 的概率。

  为什么叫似然？ 因为似然就是在给定模型参数（这里是 z）的情况下观察到某个数据 x 的可能性。在这里我们用它来评估从某个 z 生成特定 x 的概率。

  它就是 decoder，从 z 生成 x。

• $p_\theta(z \mid x)$是后验（posterior），它代表给定原始数据 x 的情况下，其潜在编码向量 z 的后验分布。换句话说，如果我们看到一个具体的 x，那么它是由什么样的 z 生成的可能性最大？

  它算不了，要用一个容易计算的近似让 encoder 给出。

$p_θ(z∣x)$ 本身就是一个分布。它描述的是在给定 x 的情况下，每一个可能的 z 值有多大的概率密度。

VAE 的核心难题（两个等价的视角）

视角一：后验分布 $p_θ(z∣x)$ 难以计算，是因为贝叶斯公式中分母 pθ(x) 难以计算。（推断潜在变量角度）

从理论上讲，编码器（Encoder）的目标就是想找到真实的后验分布 $p_θ(z∣x)$。encoder 想找到的就是一个概率分布函数，在给定一个 x 的情况下，这个函数能得到潜在空间中的每个 z 值概率密度。这个分布的“峰值”区域，就是 x 最可能对应的潜在特征。

（encoder真实情况下怎么做的？其实是先建模一个分布（一般还是高斯），然后输出参数化的概率分布（比如高斯分布的均值和方差定义）。这个过程在接下来的一张图中会展示。）

那么，$p_θ(z∣x)$ 也太难求了，因为有贝叶斯公式，

$$p_\theta(z \mid x) = \frac{p_\theta(x \mid z)p_\theta(z)}{p_\theta(x)}$$

所以假如真要去求$p_θ(z∣x)$，就要去求：

• $p_θ(x∣z)$：似然（解码器的工作），给定 z 生成 x 的概率。这个分布可以通过先选个分布（比如选择高斯分布）来建模，然后训练神经网络的参数来得到。

• $p_θ(z)$：先验，我们刚刚预设的 z 的分布，是标准正态分布，是已知的。

• $p_θ(x)$：边缘似然，在给定模型参数下，观测到特定数据点 x 的概率。唯独这个算不出来。

$p_θ(x)$ 算不出来是因为：

$$p_θ(x)=∫p_θ(x∣z)p_θ(z)dz$$

这要对所有可能的潜在向量$z$来积分。尽管相对于原始数据$x$来说，$z$已经是“压缩后”的数据了，但它仍然是高维且连续的。所以算不了。要换一种方法。

这就是我们遇到的问题。

这个问题还有另一个视角。

视角二：最大化数据对数似然 $\log p_θ(x)$困难←边缘似然 $p_θ(x(i))$困难（模型训练目标角度）

假如我们已经训练好了模型，得到了真实情况下的 $\theta^\star$，我们就可以这样来生成一个“真实”数据点$x^{(i)}$了：首先从$p_{\theta^\star}(z)$分布中抽样一个 z，然后从$p_{\theta^\star}(\mathbf{x} | \mathbf{z} = \mathbf{z}^{(i)})$分布中生成一个$x^{(i)}$。

为了能找到这参数$\theta^$，就要调整参数$\theta$，来最大化所有已知的训练数据能被以$\theta$为参数的模型生成出来的*联合概率：

$$\theta^* = \arg \max_{\theta} \prod_{i=1}^{n} p_{\theta}(x^{(i)})$$

这就是最大似然，换为对数似然求和形式，

$$\theta^* = \arg \max_{\theta} \sum_{i=1}^{n} \log p_{\theta}(x^{(i)})$$

所以我们在最大化这个：

$$p_\theta(\mathbf{x}^{(i)}) = \int p_\theta(\mathbf{x}^{(i)}\vert\mathbf{z}) p_\theta(\mathbf{z}) d\mathbf{z}$$

但刚刚才说过它算不出来。

---

解决困难：近似$p_θ(z|x)$的方法

我们引入参数为$\phi$的$q_\phi(z \mid x)$，它的输出是在给定输入 $\mathbf{x}$ 的情况下，潜变量 $\mathbf{z}$ 的概率分布（通常是一个高斯分布的参数：均值 $\mu$ 和方差 $\sigma^2$）。

$q_\phi(z \mid x)$会被用来逼近$p_\theta(z \mid x)$。

审视上面这张图中 z 与 x 的关系，发现了 auto-encoder 的结构：$p_\theta(x \mid z)$看为decoder，$q_\phi(z \mid x)$看为 encoder。

• Encoder 训练的是 $q_ϕ(z∣x)$。它是一个神经网络，输入 x，输出潜在变量 z 的近似后验分布的参数（通常是高斯分布的均值 μ 和方差 σ2）。

• Decoder 训练的是 $p_θ(x∣z)$。它也是一个神经网络，输入潜在变量 z，输出数据 x 的条件概率分布的参数（例如，如果 x 是图像，可能是伯努利分布的概率或高斯分布的均值和方差）。

---

为什么 $p_θ(x∣z)$ 可以训练而 $p_θ(z∣x)$ 不行？

• $p_θ(x∣z)$ 可以训练：
  • 在解码器中，我们给定一个已知的潜在变量 z，希望生成或重构出数据 x。这个过程是 条件概率 的建模。
  • 我们可以通过最大化重构似然（如均方误差或交叉熵）来训练解码器。例如，对于给定的 z，解码器输出 $\hat{x}$，我们希望 $\hat{x}$ 尽可能接近原始 x。这个过程是直接的，不需要计算复杂的积分。
• $p_θ(z∣x)$ 不行：
  • 如上所述,通过贝叶斯公式，计算 $p_θ(z∣x)=p_θ(x)p_θ(x∣z)p_θ(z)$ 需要知道 $p_θ(x)$，而 $p_θ(x)$ 的计算涉及到对一切的 z 的积分，这是无法解析求解的。
• 一言以蔽之：$p_θ(x∣z)$有原始数据 x 当“真实值”或“标签”，而$p_θ(z∣x)$没有能算出来的$p_θ(z∣x)$真正的原始数据当标签啊。没有标签还怎么开展监督学习？（当然，$p_θ(x∣z)$用原始数据 x 当标签是自监督学习）

为什么用 $q_ϕ(z∣x)$ 逼近 $p_θ(z∣x)$ 就解决了？

• $q_ϕ(z∣x)$ 逼近 $p_θ(z∣x)$提供了一个 可训练的替代方案。

• 我们不再直接最大化 $\log p_θ(x)$，而是转向最大化其的一个下界，也就是 证据下界（Evidence Lower Bound, ELBO）。

• $q_ϕ(z∣x)$ 到底是什么？它是一个变分分布（Variational Distribution），是一个我们引入的、易于处理的概率分布（通常是高斯分布），用来近似真实的但难以计算的后验分布 $p_θ(z∣x)$。它之所以“易于处理”，是因为它的参数（如均值 μ 和方差 $σ^2$）是由神经网络输出的。对于每个输入 x，神经网络会输出一个特定的 $μ_x$ 和 $σ_x^2$，这些参数定义了一个高斯分布 $\mathcal N(μ_x,\text{diag}(σ_x^2))$。z 会从这里被采样出来。

$q_ϕ(z∣x)$是怎么被训练的？如何构造 loss 函数？我们稍后讨论。

---

结构解释

VAE 主要步骤如上。

下面这张图就是 VAE 与一般 Auto-encoder 的对比：

采样过程与 Reparameterization Trick（重参数化技巧）

如图，VAE 中的 encoder 也会生成原始的编码（图中的$m_1\ m_2\ m_3$），它们构成了这个高斯分布的均值向量 $μ_x$。它还会生成$\sigma$，会决定向原始编码中加入 noise 的方差 variance。对$\sigma$取以 e 为底数的指数，保证方差是正的。

底下的$e_1\ e_2\ e_3$是从正态分布中取样出来的，其协方差矩阵是一个单位矩阵（因为正态分布的变量之间独立，协方差为 0）。但是，$\sigma_1\ \sigma_2\ \sigma_3$是神经网络产生的，所以它们逐元素做乘法后可以决定 noise 的大小。

最终加在一起，就是潜在向量$\mathbf{z} = \begin{bmatrix} c_1 \\ c_2 \\ c_3 \end{bmatrix}$，接下来把它送入 decoder。

这就是Reparameterization Trick。解释一下，损失函数（等一会再推导它）中的期望项，是涉及到从 $z∼q_ϕ(z∣x)$ 中生成样本。采样是一个随机过程，无法反向传播梯度，训练不了。为了可训练，引入了重参数化技巧：将随机变量 z 表示为确定性变量 $z=T_ϕ(x,ϵ)$，其中 ϵ 是一个辅助的独立随机变量，并且由 ϕ 参数化的变换函数 $T_ϕ$ 将 ϵ 转换为 z。随机性就被剥离了。

一言以蔽之，重参数化技巧将对参数化分布 $q_ϕ(z∣x)$ 的采样操作，转换成一个确定性函数，这个函数以模型参数（μ,σ）和一个固定分布的随机噪声（ϵ）为输入。关键在于 随机性（ϵ）被抽离到了一个独立于模型参数的外部变量。

公式表达就是：

$$\mathbf{z} \sim q_\phi(\mathbf{z}\vert\mathbf{x}^{(i)}) = \mathcal{N}(\mathbf{z}; \boldsymbol{\mu}^{(i)}, \boldsymbol{\sigma}^{2(i)}\boldsymbol{I})$$ $$\mathbf{z} = \boldsymbol{\mu} + \boldsymbol{\sigma} \odot \boldsymbol{\epsilon} \text{, where } \boldsymbol{\epsilon} \sim \mathcal{N}(0, \boldsymbol{I}) \scriptstyle{\text{; \ Reparameterization trick.}}$$

其中 ⊙ 表示逐元素乘法。

---

此时，如果接着采用一般的 auto-encoder 的训练方法就会出现问题，因为机器会学着把方差学成0，使潜变量退化为确定性编码，这样，会更方便它的 decoder 用编码生成图片，并产生尽量小的 reconstruction error。这有点类似机器在偷懒。

这就是“posterior collapse”（后验崩溃）问题的一种表现。

为了防止这个 ，VAE 的损失函数中的 KL 散度项 $D_{KL}(q_ϕ(z∣x)\parallel p_θ(z))$ 会惩罚这种情况。在皮卡丘那张图中，就是右下角的：

$$\text{minimize }\sum_{i=1}^{3} (\exp(\sigma_i) - (1 + \sigma_i) + (m_i)^2)$$

我们来直观看一眼这个：

首先，$\exp(σ_i)$对应的是真实方差。

先看前面两项：$e^{\sigma_i}-(1+\sigma_i)$，当$\sigma_i$为 0 时最小，所以机器会努力让$\sigma_i$为 0。此时，$exp(\sigma_i)$是 1，它与$e_i$相乘之后就是高斯分布。

机器就会权衡考虑，不能让 reconstruction error 太大，也不能让 KL 散度太小。

最后有一项$m_i^2$。这里其实是在 minimize 原始潜在编码 latent code 的二范数L2-norm，也就是加了二范数的正则化 regularization。

这会让它的结果比较稀疏 sparse，不会 overfitting，不会 learn 出太多无意义的无效解 trivial solution。

但以上都是对公式的直观理解。正式解释要推导一下 VAE 的 loss 函数。我们接下来就来学习一下。

VAE 的 loss 函数（两种等价的方法推导）

方法一：从最大化数据对数似然 $logp_θ(x)$ 出发（变分推断视角）

先以 Gaussian mixture model 引入（注意它不是 loss 函数）

现在以生成宝可梦的图片为例，一维的向量 x 对应着每张宝可梦图。现在在做的事情就是预测 P(x)，就是根据 x 的概率分布，找到概率高的向量，生成出来的就会是宝可梦的样子。

如何 estimate 一个概率分布呢？可以用 Gaussian mixture model。将概率分布视为很多个高斯分布按照不同的权重叠加起来的结果。也就是：

$$P(x)=\sum_m{P(m)P(x\parallel m)}$$

如果要从 P(x) 中采样，就要先根据 P(m) 来决定从哪一个高斯分布中取样（这就是每一个高斯分布的权重）。然后再从选定的高斯分布来采样。步骤如图：

采样步骤的公式就是：

$$m \sim P(m) \quad \text{(multinomial)}$$ $$x \mid m \sim \mathcal{N}(\mu^m, \Sigma^m)$$

每一个 x 是来自于不同的高斯分布的。这就有点像是分类任务，因为 data 来自不同的 class。

然而，分布式表示（distributed representation）优于聚类（cluster）表示。有一个人，他一半是艺术家，一半是程序员，就没法被归类。但是，用分布式表示的向量来表示这个人，就可以叫他[0.5, 0.5]，第一个维度代表艺术家，第二个维度代表程序员。

在高斯混合模型中，”计算数据点属于每个高斯分量的概率“这个步骤看起来有点”分布“了。

所以，我们回到 VAE，它其实就是 Gaussian mixture model 的 distributed representation 版本。Distributed representation 就是一个概念由多个维度的组合来编码的。

模型	每个样本如何表示？	潜在空间是…
GMM（高斯混合模型）	属于某个高斯（离散标签）	离散的几个高斯分布
VAE	一个向量（分布式）	连续的潜在空间（通常是标准正态）

loss 函数推导

我们首先从正态分布中抽样一个 z，它是一个向量，不同维度代表不同attribute特质。

根据 z，再决定抽样 x 的高斯分布，也就是：

$$z \sim N(0,I)$$ $$x \mid z \sim \mathcal{N}(\mu(z), \sigma(z))$$

z 可以决定高斯分布的平均值和方差。

在刚刚的 Gaussian mixture model 中，mean 与 variance 就是确定的那几类。但是现在的 VAE 中，由于 z 是连续的、无穷多的，所以平均值和方差可能性就更多了。

如何给定 z 来确定$\mu,\sigma$？用神经网络训练出输入z、输出$\mu,\sigma$的函数即可。

p(x) 就是：

$$p(x)=\int_z p(z)p(x\mid z)dz$$

p(x) 是在模型下，包括潜在变量 z 和生成过程，观测到特定数据点 x 的概率。

简单来说，p(x) 衡量的是：一个真实存在的数据 x，有多大的可能性是由模型生成的？ 如果可能性越大，说明模型越能解释这个数据。

它是通过对所有可能的潜在变量 z 进行积分得到的，即考虑了所有可能的“内在原因” z 如何导致了 x 的生成。它就是边缘似然（Marginal Likelihood）。

对于边缘似然，有一些容易误解的点，我现在要明确一下。下面这些解释可以结合之前那张图看，我也搬过来：

我们来解释一下：

• $p_\theta(x)$ 是一个函数，是一个概率密度函数（PDF），它描述了在给定模型参数 θ 的情况下，随机变量 x 的概率分布，即给出了在模型参数 θ 下，任何一个可能的输入 x 的概率密度。它就是模型认为真实数据应该如何分布。
• 当训练 VAE 时，我们提供了一批真实的训练数据 $x^{(1)},x^{(2)},…,x^{(N)}$。目标是调整 VAE 的参数 θ（解码器参数）和 ϕ（编码器参数），使得模型的 $P_θ(x)$ 能够尽可能地高地给这些真实的训练数据赋值。
  • 如果模型学习得好，那么对于一个真实的 $x^{(i)}$，模型会给出较高的 $p_θ(x(i))$。
  • 如果模型学习得好，那么对于一个不真实或随机的图片 $x_\text{noise}$，模型会给出较低的 $p_θ(x_\text{noise})$。
  • 最终，希望模型学到的分布能够近似真实数据的分布 $p_\text{data}(X)$。
• 注意“生成”和“评估”的区别：
  • 当 VAE 在生成模式下工作时，我们从先验 $p(z)$ 中（这个是标准正态分布）采样一个 z，然后用解码器 $p_\theta(x∣z)$ 生成样本$x’$ 。
  • 而我们讨论的p(x) 是在评估（或者说训练）模型的过程中，衡量模型对已存在的真实数据的解释能力。

最大化 $p_\theta(x)$ 可以让模型更好地学习到真实数据 x 的分布。

现在的问题是如何训练神经网络找到$\mu(z), \sigma(z)$。训练这个神经网络的评判标准 criterion 和之前学的大多数神经网络的一样，也是去进行最大似然估计，maximize likelihood。我们刚刚在“核心难题”的“视角二”里面已经写过了这一部分，再写一下：

我们要最大化观测到的 x 的似然，$\theta$是产生$\mu(z), \sigma(z)$的神经网络的参数，

$$\text{likelihood}(\theta | \mathbf{X}) = \prod_{i=1}^{N} P(x_i | \theta)$$

取对数似然，

$$L = \log \text{likelihood}(\theta | \mathbf{X}) = \sum_{x \in \text{dataset}} \log P(x | \theta)$$

我们引入另一个分布$q(z\mid x)$，经过神经网络训练，它可以在给定$x$的情况下，可以决定$z$要从什么样的均值与方差的正态分布中 sample 出来。

这两个神经网络就是 VAE 的 Decoder 和 Encoder，如图：

接下来对变分下界（Evidence Lower Bound, ELBO）的推导与 Diffusion Model 的很像。

$$\log P(x)=\int_zq(z\mid x)\log p_\theta(x)dz$$ $$原式= \int_z q(z \mid x)\log(\frac{p_\theta(z,x)}{p_\theta(z \mid x)})dz$$ $$原式= \int_z q(z \mid x)\log(\frac{p_\theta(z,x)}{q(z \mid x)}\frac{q(z \mid x)}{p_\theta(z \mid x)})dz$$ $$原式= \int_z q(z \mid x)\log(\frac{p_\theta(z,x)}{q(z \mid x)})dz+\int_z q(z \mid x)\log(\frac{q(z\mid x)}{p_\theta(z \mid x)})dz$$

右边那项是 KL 散度，

$$原式= \int_z q(z \mid x)\log(\frac{p_\theta(z,x)}{q(z \mid x)})dz+ D_{KL}(q(z \mid x) \parallel p_\theta(z \mid x))$$

KL 散度大于等于0，

$$原式≥ \int_z q(z \mid x)\log(\frac{p_\theta(z,x)}{q(z \mid x)})dz$$

不等号右侧就是 lower bound，记作$L_b$，

$$\log p_\theta(x)= L_b +D_{KL}(q(z \mid x) \parallel p_\theta(z \mid x))$$ $$L_b=\int_z q(z \mid x)\log(\frac{p_\theta(x \mid z)p_\theta(z)}{q(z \mid x)})dz$$

由于

$$\log P(x)= L_b +D_{KL}$$

而$p_\theta(x)$只与$p_\theta(x\mid z)$有关：

$$P(x)=\int_z P(z)P(x\mid z)dz$$

所以，如果我们maximize $L_b$，KL 散度会变小，q(z|x) 与 P(z|x)越来越接近。

由于 真实后验分布$p_\theta$(z∣x) 的分母 $p_\theta$(x) 难以计算，导致我们无法直接得到真实的后验分布 $p_\theta$(z∣x)。但我们可以用 q(z|x) 来估算。

继续推导证据下界（Evidence Lower Bound, ELBO），有

$$L_b=\int_z q(z \mid x)\log(\frac{p_\theta(x \mid z)p_\theta(z)}{q(z \mid x)})dz$$ $$=\int_z q(z \mid x)\log(\frac{p_\theta(z)}{q(z \mid x)})dz+\int_z q(z \mid x)\log p_\theta(x \mid z)dz$$ $$=-D_{KL}(q(z \mid x) \parallel p_\theta(z))+\int_z q(z \mid x)\log p_\theta(x \mid z)dz$$

要maximize $L_b$，就要 minimize 前面一项 KL 散度，并maximize 后面那一项。

先看 minimize KL 散度。给 q 对应的神经网络 x，它会说 z 是从什么样的均值、方差的高斯分布里采样的。现在如果要minimize，就要让 q 对应对应的神经网络让它产生的分布与一个$p_\theta(z)$也就是标准正态分布越接近越好。

这个就是 VAE 引入的 KL 散度项。也就是那张皮卡丘图的右下角。

再看 maximize 这个：

$$\int_z q(z \mid x)\log p_\theta(x \mid z)dz$$

有：

$$\int_z q(z \mid x)\log p_\theta(x \mid z)dz = E_{q(z \mid x)}[\log p_\theta(x\mid z)]$$

那么就是先对 z 采样（因为q(z|x)）。先用 x 输入到 encoder 里面，用产生的$\mu’(x)$与$\sigma’(x)$对应的分布来采样 z，然后输入 decoder，它会 output 出$\mu(x)$与$\sigma(x)$，它们两所代表的 distribution 产生的 x 的概率就是上式里的$p_\theta(x\mid z)$了。

怎么让它 maximize 呢？

忽视方差，让平均值与 x 越接近，$p_\theta(x\mid z)$越大。

这就是 auto-encoder 的工作，因为这个的 loss 就是重建误差呀。

上面这两项的结果合起来，就是 VAE 的 loss 了，即

$$\begin{equation} \mathcal{L}_{\text{VAE}} = \underbrace{\mathbb{E}_{q_\phi(z|x)}[\log p_\theta(x|z)]}_{\text{重建误差（Reconstruction Loss）}} - \underbrace{D_{KL}(q_\phi(z|x) \,||\, p(z))}_{\text{正则项（KL 散度）}} \end{equation}$$

	普通 Autoencoder	变分自编码器 VAE
loss 函数	$\mathcal{L}_{\text{AE}} = ‖x - \hat{x}‖^2$或$-\log p_\theta(x \mid z)$	$\mathcal{L}_{\text{VAE}} = \mathbb{E}_{q_\phi(z \mid x)}[\log p_\theta(x \mid z)] - D_{KL}(q_\phi(z \mid x) ‖p(z))$
编码器输出	固定向量 z	分布 $ \mathcal{N}(\mu, \sigma^2) $，并从中采样
隐变量 z	直接使用	使用重参数化采样
正则项	无 KL 散度	有 KL 散度正则化
生成能力	差，无法生成新样本	强，可从 p(z) 中采样生成新样本
隐空间结构	不连续、无语义	连续、有语义
训练难度	简单	稍复杂（需采样 + KL）

等等，这个真的也解决了用$q_\phi(z \mid x)$近似$p_\phi(z \mid x)$的难题吗？

我们回顾一下 VAE 的核心等式：

$$\log p_θ(x)=ELBO+D_{KL}(q_ϕ(z∣x)∥p_θ(z∣x))$$

KL 散度的一个性质是非负。我们的最终目标 是最大化 $\log p_θ(x)$，并由于前面提到的难题，我们转而最大化 ELBO。

在训练过程中，对于一个给定的真实数据点 x，真实的 $\log p_θ(x)$ 是一个我们无法直接计算但客观存在的量。在理想情况下，我们希望模型学到的 θ 能使这个 $\log p_θ(x)$ 尽可能大。

当我们最大化 ELBO 时，那么为了保持等式成立，并且由于 $D_{KL}$ 不能是负数，它就必须变得越来越小。$\log p_θ(x)$ 是一个“上限”（虽然它也在变化，但我们可以把它看作一个目标），我们通过最大化 ELBO 来“逼近”这个天花板。当努力把下界（ELBO）推高时，下界和天花板之间的距离（KL 散度）自然就会减小。

方法二：从最小化近似后验与真实后验的 KL 散度出发（近似推断视角）

这个方法更侧重于直接看 $q_ϕ(z∣x)$ 与 $p_θ(z∣x)$ 的 KL 散度。

我们用$D_\text{KL}(q_\phi | p_\theta)$而不是$D_\text{KL}(p_\theta | q_\phi)$，即用 reversed KL 而不是 forward KL。这个的原因我在 KL 散度的学习笔记里有写。或者可以看这张图：

loss 函数推导的具体步骤可以看From Autoencoder to Beta-VAE | Lil’Log。