Diffusion Model学习笔记

现在，参考 DDPM 的论文和李宏毅老师 的课程，我会深入浅出地记录我学习 Diffusion Model 的笔记。

先简略学习diffusion model的概念

以下主要学习知名的 Denoising Diffusion Probabilistic Model，DDPM。它是 diffusion model 的奠基之作，论文在arxiv的地址是 Denoising Diffusion Probabilistic Models 。

先从高斯分布 中，sample出一个都是杂讯的图片。接下来，通过denoise 的神经网络，去除杂讯，得到清晰的图片。denoise 的次数是事先定好的。这个步骤就是Reverse Process 。

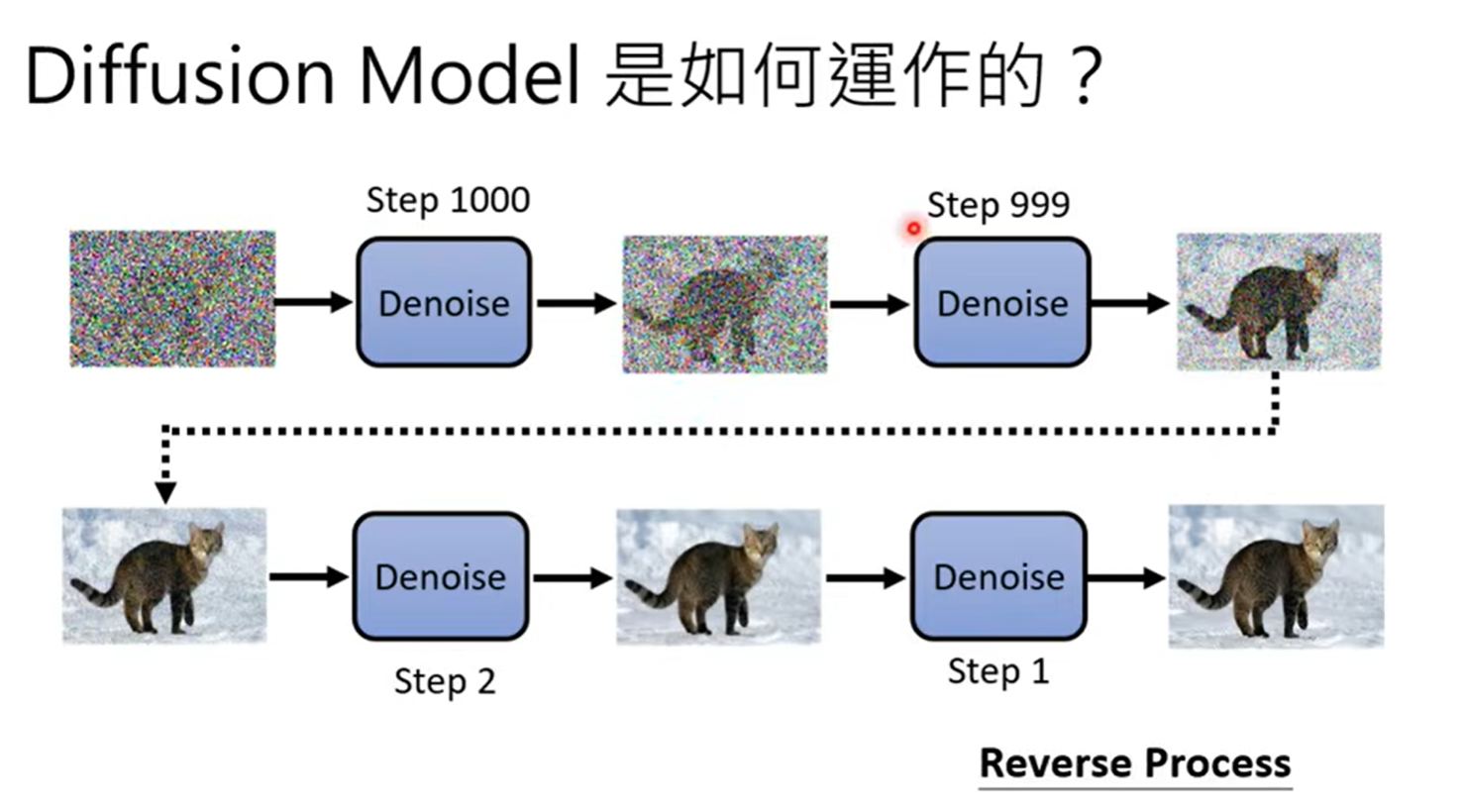
这里是把同一个denoise的model反复进行使用。然而，由于图片在reverse process的过程中，包含的杂讯不同，所以denoise在输入图片的时候，还需要输入这是第几个step， 这个信息代表杂讯的严重程度。现在我们来具体了解一下denoise的内部。

denoise内部有noise predicter ，向它输入图片、输入step，它的作用是输出预测图片中杂讯是什么样子的。用原图像减去noise predicter的预测杂讯，就能得到deniose的结果。

怎么训练这个noise predicter呢？问题主要如何获得在Ground truth 进行训练。这些噪声、含噪声的图片是人为生成的，过程与Reverse Process是相反的，如图，这个过程叫forward process或diffusion process。

（当然，等我写到后面的数学部分，其实就会发现不是这样“一步步”加噪声的，这里这样表示是便于理解。）

然而，我们需要的不仅仅是生成图片。刚才讨论的只有从杂讯里生成图片，没有考虑到text-to-image的人物。如何通过一句“a cat in the snow”的prompt来生成上面的这张实例图片呢？

首先了解一下laion 。LAION（Large-scale Artificial Intelligence Open Network） 是一个德国的非营利组织，致力于构建和开放发布大规模人工智能训练数据集，尤其是用于训练多模态模型 图像+文本数据。这就是如何获取图文数据。

在text-to-image的任务中，我们只需要将文字加到denoise的模组就可以了。

训练的过程如下：

在DDPM的原论文中，对这个算法的伪代码是：

Algorithm 1: Training

1. repeat

2.     $x_0 \sim q(x_0)$

3.     $t \sim \text{Uniform}(\{1, \dots, T\})$

4.     $\epsilon \sim \mathcal{N}(0, \mathbf{I})$

5.     Take gradient descent step on:

   $$\nabla_\theta \left\| \epsilon - \epsilon_\theta\left( \sqrt{\bar{\alpha}_t} \, x_0 + \sqrt{1 - \bar{\alpha}_t} \, \epsilon, \, t \right) \right\|^2$$

6. until converged

Algorithm 2: Sampling

1. $x_T \sim \mathcal{N}(0, \mathbf{I})$
2. for $t = T, \dots, 1$ do
3.     Sample $z \sim \mathcal{N}(0, \mathbf{I})$ if $t > 1$, else $z = 0$
4.     Compute:

$$x_{t-1}=\frac{1}{\sqrt{\alpha_t}} \left( x_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \epsilon_\theta(x_t, t) \right) + \sigma_tz$$

1. end for
2. return $x_0$

以上是对DDPM 的简单了解。现在我来详细学习一下DDPM 背后的原理。

Diffusion Model 原理

这张图可以很好地对比 VAE 和 Diffusion，

现在，我来从DDPM论文 Denoising Diffusion Probabilistic Models 的伪代码入手学习。

Training

Algorithm 1: Training

1. repeat

2.     $x_0 \sim q(x_0)$

3.     $t \sim \text{Uniform}(\{1, \dots, T\})$

4.     $\epsilon \sim \mathcal{N}(0, \mathbf{I})$

5.     Take gradient descent step on:

   $$\nabla_\theta \left\| \epsilon - \epsilon_\theta\left( \sqrt{\bar{\alpha}_t} \, x_0 + \sqrt{1 - \bar{\alpha}_t} \, \epsilon, \, t \right) \right\|^2$$

6. until converged

我们逐行来看。

repeat until converged 是循环直到收敛。

第二行做的事情是，先 sample 出一个 image 为 $x_0$ 。这个图像是“干净”的，是最后要生成的图片。$q(x_0)$ 是资料库。

第三行是，从 1 到 T 中，等概率地随机选一个整数 t。

第四行是，从高斯分布（均值为 0，协方差矩阵为单位矩阵）里sample 出来一个噪声向量ϵ。

第五行需要深入理解一下，里面有很多设计：
我们有一张干干净净的原图 $x_0$，现在往里面加上一些随机噪声，得到一张被污染了的图像 $x_t$。
这个加噪公式是：

$$x_t = \sqrt{\bar{\alpha}_t} \cdot x_0 + \sqrt{1 - \bar{\alpha}_t} \cdot \epsilon$$

这个公式其实就是 $x_0$ 和ϵ的weighted sum。这里的weight，$\bar{\alpha}_t$，是一个跟时间步 t 有关的系数，表示“保留原图多少信息”。从 $\bar{\alpha}_1$，$\bar{\alpha}_2$ 到 $\bar{\alpha}_T$，都是我们实现定好的一组weight。 $x_0$ 和ϵ做加权和之后就能得到一个有噪声的图片 $x_t$。

要注意设计中，从 $\bar{\alpha}_1$，$\bar{\alpha}_2$ 到 $\bar{\alpha}_T$ 是逐步减小的。t越大代表 $\bar{\alpha}_t$ 越小，则有噪声的图片中，原图的比例也会越小，噪声的比例会越大。

现在来看这个有一点复杂的noise predictor：

$$\epsilon_\theta\left( \sqrt{\bar{\alpha}_t} \, x_0 + \sqrt{1 - \bar{\alpha}_t} \, \epsilon, \, t \right)$$

将有噪声的图片与 t 作为 $\epsilon_\theta$ 的输入。 $\epsilon_\theta$ 会根据输入，猜测加入的噪声是什么样的。将ground truth，也就是刚刚的 $\epsilon$ ，与它相减 ，求二范数的平方，就是它的损失函数（MSE loss）了，如下：

$$loss=\left\| \epsilon - \epsilon_\theta\left( \sqrt{\bar{\alpha}_t} \, x_0 + \sqrt{1 - \bar{\alpha}_t} \, \epsilon, \, t \right) \right\|^2$$

接下来，对这个 loss 函数进行梯度下降就可以了：

$$x\nabla_\theta \left\| \epsilon - \epsilon_\theta\left( \sqrt{\bar{\alpha}_t} \, x_0 + \sqrt{1 - \bar{\alpha}_t} \, \epsilon, \, t \right) \right\|^2$$

以上就是 Diffusion Model 进行 Training 的全过程。但是，为什么是这样？为什么要这样？可以从数学上对此进行推导吗？我会在稍后说明，先看看第二个算法，它可以用来产生图片：Sampling

Sampling

Algorithm 2: Sampling

1. $x_T \sim \mathcal{N}(0, \mathbf{I})$

2. for $t = T, \dots, 1$ do

3.     $z \sim \mathcal{N}(0, \mathbf{I})$ if $t > 1$, else $z = 0$

4.     

   $$x_{t-1} = \frac{1}{\sqrt{\alpha_t}} \left( x_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \, \epsilon_\theta(x_t, t) \right) + \sigma_t z$$

5. end for

6. return $x_0$

我们也对此来逐行分析。

第一行，先从高斯分布中sample出一个纯粹全是noise的图，它就是$x_T$。

第二行开始一个 for 循环，循环变量 t 从 T 到 1。

第三行开始进入了 for 循环内部。又sample一个全是noise的图，它就是$z$。不过，当循环变量 t 等于 1 的时候，$z$是 0。

第四行展现了循环内迭代的过程。$x_{t-1}$ 是本步骤产生的图，$x_{t}$ 是上一个步骤产生的图。先看括号里面这个：

$$x_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \, \epsilon_\theta(x_t, t)$$

$\epsilon_\theta(x_t, t)$ 是noise predictor输出的noise，用$x_t$ 减去 $\frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \, \epsilon_\theta(x_t, t)$ ，$\epsilon_\theta(x_t, t)$ 被减之前乘上了常数$\frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}}$，这个的大小也取决于现在是第几个迭代（注意下标t）。剪完之后，乘上$\frac{1}{\sqrt{\alpha_t}}$，再加上$\sigma_t z$。

$\alpha_t, \bar{\alpha}_t, \sigma_t$ 是在DDPM设计时预先定义的权重和方差系数，决定加噪和去噪的比例。我们会在稍后讨论它们。

这个算法过程可以用这张图表示：

接下来，我们来探究一下结构设计背后的本质原因。

用数学来分析结构

影像生成模型本质共同目标

从一个 distribution 中 sample 出一个 vector z，放入神经网络 G，生成图片 x。这个过程可以用这张图表示：

这个神经网络的生成要与真图片越接近越好。

还有的network可以允许你输入文字来生成图片，

结构没有什么不同。我们接下来的推导假设模型没有文字输入condition。

Maximum Likelihood Estimation 与 从MLE推导出KL散度

刚刚我们提到，我们生成的 $x$ 要与真实图片越接近越好。与真实越接近越好？这听起来是不是概率论中的最大似然估计（Maximum Likelihood Estimation，MLE） ？

我们先简单回顾一下最大似然估计。

现在我有一枚硬币。它是特制的，有可能一面是数字 $1$，一面是花；有可能两面都是数字 $1$；有可能两面都是花。

假设抛硬币的结果是数字朝上的概率是 $p$， $p$ 在目前是未知的。最大似然估计就是：找到 $p$ 使得“观察到真实数据出现”的概率最大。

例如，我抛了十次硬币，全是数字 $1$ 朝上，每次都是独立事件，概率就是：

$$L(p)=p^{10}$$

这就是似然函数（Likelihood），表示在给定 $p$ 的情况下，数据出现的概率。我们只需要找到让 $L(p)$ 最大的 $p$ 就可以了，在这个例子里，显然 $p=1$ 时 $L(P)$ 最大。这就是说，最大似然估计的 $p$ 是 1，估计硬币正面的概率是 1。

因此，这枚特制的硬币，最大似然估计的 $p$ 是 1，那么极有可能两面都是数字。总结一下，MLE 是一种“逆推参数”的方法。观察到数据，再选让数据最有可能出现的参数。

现在来看看 MLE 在影像生成中是如何作用的：

如上图，我们从 $P_{data}(x)$ 中 sample 出来一个 $\{x^1, x^2, …, x^m\}$，这是一堆训练资料图像。现在做一个假设：假设我们能计算出来 $p_\theta(x^i)$ ，即通过参数为 $\theta$ 的神经网络的分布产生 $x^i$ 的几率。但注意，这件事是可能做不到的，它是一个复杂的distribution。怎么可能随便给你一张图 $x^i$ 你就能算几率？我们先这样假设着。

现在，我们要找的 $\theta^*$ 就是使 $P_\theta(x^i)$ 之积最大的 $\theta$​。右下角这个公式就是最大似然函数 的标准形式：

$$\theta^* = \arg \max_\theta \prod_{i=1}^{m} P_\theta(x^i)$$

MLE让图像“接近”的关联性究竟是什么呢？回忆以前的机器学习知识，想起对最大似然函数最标准最常见的处理方法是取负对数，这里我们也对它取对数，过程就是：

$$前提：\text{Sample } \{x^1, x^2, ..., x^m\} \text{ from } P_{data}(x)$$ $$\theta^* = \arg \max_{\theta} \prod_{i=1}^{m} P_{\theta}(x^i)$$ $$= \arg \max_{\theta} \log \prod_{i=1}^{m} P_{\theta}(x^i)$$ $$= \arg \max_{\theta} \sum_{i=1}^{m} \log P_{\theta}(x^i)$$ $$\approx \arg \max_{\theta} E_{x \sim P_{data}}[ \log P_{\theta}(x)]$$

等等！这一步是什么？事实上，$E_{x \sim P_{data}}[ \log P_{\theta}(x)]$ 代表从数据的真实分布 $P_{\text{data}}$​ 采样，然后取期望。如果“不断的找图”，m足够大，这是可以近似的，

$$m→∞时，\frac{1}{m} \sum_{i=1}^{m} \log P_\theta(x^i) \approx \mathbb{E}_{x \sim P_{data}}[\log P_\theta(x)]$$

那我们继续往下。由期望的定义，得

$$\theta^*\approx \arg \max_{\theta} E_{x \sim P_{data}}[ \log P_{\theta}(x)]$$ $$= \arg \max_{\theta} \int_{x} P_{data}(x) \log P_{\theta}(x)dx$$

由于$\int_{x} P_{data}(x) \log P_{data}(x)dx$ 是与 $\theta$ 无关的，因此有

$$上式=\arg \max_{\theta} \int_{x} P_{data}(x) \log P_{\theta}(x)dx - \int_{x} P_{data}(x) \log P_{data}(x)dx$$ $$= \arg \max_{\theta} \int_{x} P_{data}(x) \log \frac{P_{\theta}(x)}{P_{data}(x)}dx$$

好熟悉啊，这不是我在GAN学习笔记里面学过的KL散度 （Kullback-Leibler Divergence）吗？回顾一下吧，对于两个概率分布 P(x) 和 Q(x)，KL 散度 的定义是：

$$D_{\mathrm{KL}}(P \parallel Q) = \sum_x P(x) \log \frac{P(x)}{Q(x)}$$

在刚刚的式子中是连续分布，所以用积分替代求和。其中：

• P(x)：真实的分布（观测到的）
• Q(x)：用来近似的分布（模型预测的）
• 如果 P = Q，那么 KL 散度为 0，表示“完美近似”
• KL 散度越大，表示 Q 假装成 P 的能力越差

因此，

$$\text{Maximum Likelihood = Minimize KL Divergence}$$

我们从最大似然推导出了最小化 KL 散度，而 KL 散度 $D_{KL}(P_{data}∥P_θ)$ 最小时表示模型分布$P_\theta(x)$ 越来越像真实数据分布 $P_{\text{data}}$。这就解释清楚了MLE可以图像“接近”真实数据的关联性。

VAE（变分自编码器，Variational Autoencoder）计算 $P_\theta(x)$ 的方法与优化目标

VAE与 diffusion model 非常相似，这里也简单了解一下。这些图足够概括了：

第一张图解释了VAE如何计算生成模型的概率$P_\theta(x)$，第二张图通过推导，解释了maximize右下角的lower bound可以让$P_\theta(x)$得到max。为什么要让$P_\theta(x)$得到max？这里和之前的想法是一样的，因为 $x$ 代表真实数据点（观测数据）。

DDPM 计算 $P_\theta(x)$ 的方法与优化目标

那我们继续来看DDPM。如果把denoise的结果想象成 高斯分布的mean，就可以得到：

顺便解释一下，DDPM和VAE的∝exp(……)是由高斯分布推导的，这里不展开解释。

接下来，和VAE推导过程完全相同，就能得到DDPM的lower bound。

在 VAE 中，$q(z∣x)$ 是encoder“学习”来近似真实后验的分布。

为什么？？ 上面推导lower bound的过程的那张图，绿色框框里不是说 $q(z∣x)$ 可以是任何分布吗？

这是因为我们是为了引入一个“近似后验”分布 $q(z|x)$，来近似真正的后验 $P(z|x)$，从而对这个 log-likelihood 建立一个lower bound。

注意， $q(z|x)$ 是用来近似真正的后验的，那么 $q(z|x)$ 就应该是encoder。

在 DDPM 中，$q(x_1:x_T∣x_0)$ 是diffusion process的分布。

我们接下来关注$q$的计算。

$q(x_t∣x_{t-1})$ 的计算

在DDPM中，$x_{t}$ 与 $x_{t-1}$ 的迭代关系是：

$$x_{t} = \sqrt{1 - \beta_t} \cdot x_{t-1} + \sqrt{\beta_t} \cdot \epsilon \quad \text{其中} \quad \epsilon \sim \mathcal{N}(0, I)$$

其中，$\beta_1, \beta_2, …, \beta_T$ 是预先定好的，noise 是从高斯分布sample出来的。

所以，$x_{t}$的distribution依然可以看为一个高斯分布，也就是：

$$x_{t} \sim \mathcal{N}\left( \sqrt{1 - \beta_t} \cdot x_{t-1}, \beta_t \cdot I \right)$$

而 $q(x_t∣x_{t-1})$ 就是 $x_t$ 的分布distribution呀，因此，$q(x_t∣x_{t-1})$ 就是上面所表示的高斯分布，它的均值 mean 是$\sqrt{1-\beta_t}x_{t-1}$，它的方差 variance 是$βt⋅I$。

接下来，该怎么算 $q(x_t|x_0)$ 呢？事实上，这个的计算方法，不是 一开始概述部分“一步步”加噪声的方法。

由于每一次从高斯分布 $\mathcal{N}(0, I)$ 中sample 出来的噪声是独立（independent）的，我们可以把$x_1$ 的表达式带入 $x_2$ 的计算过程，也就知道了 $x_2$ 与 $x_0$ 的关系，如图，

为什么可以这样？证明如下：

$$\text{Let } Z = a\epsilon_1 + b\epsilon_2$$ $$\text{where } \epsilon_1 \sim \mathcal{N}(0, I), \epsilon_2 \sim \mathcal{N}(0, I) \text{ are independent.}$$ $$a = \sqrt{1-\beta_2}\sqrt{\beta_1}, \quad b = \sqrt{\beta_2}$$ $$E[Z] = aE[\epsilon_1] + bE[\epsilon_2] = a \cdot 0 + b \cdot 0 = 0$$ $$Var[Z] = Var[a\epsilon_1 + b\epsilon_2]$$ $$= a^2 Var[\epsilon_1] + b^2 Var[\epsilon_2]$$ $$= (\sqrt{1-\beta_2}\sqrt{\beta_1})^2 I + (\sqrt{\beta_2})^2 I$$ $$= (1-\beta_2)\beta_1 I + \beta_2 I$$ $$= (\beta_1 - \beta_1\beta_2 + \beta_2) I$$ $$= (1 - (1-\beta_1)(1-\beta_2)) I$$ $$\therefore Z \sim \mathcal{N}(0, (1 - (1-\beta_1)(1-\beta_2)) I)$$ $$\text{By standardization, } Z = \sqrt{1 - (1-\beta_1)(1-\beta_2)} \cdot \epsilon_{new}$$ $$\text{where } \epsilon_{new} \sim \mathcal{N}(0, I)$$ $$证毕$$

说句题外话，有没有觉得这里有点像没有激活函数 的神经网络呀？

在神经网络中，如果没有激活函数，那么无论网络有多少层，最终的输出都将是输入的一个线性组合。

也就是说，整个深度神经网络的计算过程，可以被简化为一个大的矩阵乘法（加上一个偏置项）。

一个例子：假设有一个简单的两层神经网络，

$$第一层：h_1=W_1x+b_1$$ $$第二层：h_2=W_2h_1+b_2$$

如果我们令

$$W_{new}=W_2W_1$$

以及

$$b_{new}=W_2b_1+b_2$$

那么就有

$$h_2=W_{new}+b_{new}$$

因此，对于没有激活函数的神经网络，无论它的层数有多深，都不过只能拟合出一个单层的线性模型。

这就是为什么我们需要在深度神经网络中引入非线性激活函数。

最终，就会变为：

我们就这么导出了 $\bar{a}_t$。

Minimize Lower Bound

了解了 $q$ 的计算后，我们接下来的任务是最小化lower bound。具体过程如图，较为复杂。

我们来关注最后的结果，即

$$\text{lower bound of } logP(x)\\ E_{q(x_1|x_0)}\left[\log P(x_0|x_1)\right] - KL\left(q(x_T|x_0)||P(x_T)\right) - \sum_{t=2}^{T} E_{q(x_t|x_0)}\left[KL\left(q(x_{t-1}|x_t, x_0)||P(x_{t-1}|x_t)\right)\right]$$

我们来看这里面的三项。

第一项几率分布是 $q(x_1|x_0)$ ，对 $logP(x_0|x_1)$ 取期望；

第二项是 $q(x_T|x_0)$ 与 $P(x_T)$ 之间的KL散度，这一项与 network 的参数 $\theta$ 没有关系，为什么？因为 $P(x_T)$ 是从高斯分布中取的杂讯，network不会影响高斯分布呀，而 $q(x_T|x_0)$ 与network也没有关系，它是diffusion process，是一条人为设计的固定的马尔科夫链，与网络的训练没有关系，因此这一项我们无视它；

这一部分容易忘了刚才对 $q$ 的推导，我们回顾一下：

正向扩散过程（diffusion process）是一个人为设计的固定的马尔可夫链，从真实样本 $x_0$ 一步步加入噪声直到最后一个时间步 $x_T$，即：

$$q(x_{1:T} | x_0) = q(x_1|x_0) q(x_2|x_1) \cdots q(x_T | x_{T-1})$$

这一过程中的每一步 $q(x_t | x_{t-1})$ 都是预定义的高斯分布，在上面我们推导过，

$$q(x_t|x_{t-1})=\mathcal{N}\left(x_t; \sqrt{1 - \beta_t} \cdot x_{t-1}, \beta_t \cdot I \right)$$

整个 $q$ 过程是固定的、与神经网络无关。

第三项有点复杂，期望的几率分布是 $q(x_t|x_0)$ ，期望是$q(x_{t-1}|x_t,x_0)$ 与 $P(x_{t-1}|t_t)$ 的KL散度，这与network有关。

我们关注如何优化第三项，来让 lower bound 最小。第一项方法类似，不细讲。

第三项是

$$- \sum_{t=2}^{T} E_{q(x_t|x_0)}\left[KL\left(q(x_{t-1}|x_t, x_0)||P_\theta(x_{t-1}|x_t)\right)\right]$$

$q(x_{t-1}|x_t,x_0)$ 是什么？是 给定带噪样本 $x_t$ 和原始样本 $x_0$ 的情况下，前一步 $x_{t-1}$ 的真实后验分布 。即：在我们知道起点 $x_0$ 和当前时间步 $x_t$ 的前提下，$x_{t-1}$ 的真实条件分布。

而我们之前会算的，只有 $q(x_{t}|x_0)$ ，$q(x_{t-1}|x_0)$ 和 $q(x_{t}|x_{t-1})$ ，它们都是diffusion process的前向传播过程（或其累积分布），所以我们好推导出它们的计算公式，即

$q(x_{t-1}|x_t,x_0)$ 让我们已经看到了最开始纯洁无暇的 $x_0$ 与有了一些噪声的 $x_t$，而它们中间的过程是不知道的，要求推导出 $x_{t-1}$ 的分布。

我们能试着导出吗？事实上，过程是这样的：

$$q(x_{t-1}|x_t,x_0) \\$$ $$= \frac{q(x_{t-1},x_t,x_0)}{q(x_t,x_0)} \\$$ $$= \frac{q(x_t|x_{t-1})q(x_{t-1}|x_0)q(x_0)}{q(x_t|x_0)q(x_0)} \\$$ $$= \frac{q(x_t|x_{t-1})q(x_{t-1}|x_0)}{q(x_t|x_0)}$$

$q(x_{t}|x_0)$ ，$q(x_{t-1}|x_0)$ 和 $q(x_{t}|x_{t-1})$ 这三项高斯分布的 mean 和 方差都是我们知道的，我们带入，过程如图，

过程好长啊，最后的结果是一个高斯分布，

$$q(x_{t-1} | x_t, x_0) = \mathcal{N}(x_{t-1}; \tilde{\mu}_t(x_t, x_0), \tilde{\beta}_t I)$$

其中，

$$\tilde{\mu}_t(x_t, x_0) = \frac{\sqrt{\bar{\alpha}_{t-1}} \beta_t}{1 - \bar{\alpha}_t} x_0 + \frac{\sqrt{1 - \beta_t} (1 - \bar{\alpha}_{t-1})}{1 - \bar{\alpha}_t} x_t$$ $$\tilde{\beta}_t = \frac{1 - \bar{\alpha}_{t-1}}{1 - \bar{\alpha}_t} \beta_t$$

我们总算得到了 $q(x_{t-1} | x_t, x_0)$，现在可以继续计算

$$KL\left(q(x_{t-1}|x_t, x_0)||P_\theta(x_{t-1}|x_t)\right)$$

而两个高斯分布的KL散度计算公式是

$$D_{\text{KL}}\left(\mathcal{N}(\boldsymbol{x}, \boldsymbol{\mu_x}, \boldsymbol{\Sigma_x}) \| \mathcal{N}(\boldsymbol{y}, \boldsymbol{\mu_y}, \boldsymbol{\Sigma_y})\right) = \frac{1}{2} \left[\log \frac{|\boldsymbol{\Sigma_y}|}{|\boldsymbol{\Sigma_x}|} - d + \text{tr}(\boldsymbol{\Sigma_y^{-1}\Sigma_x}) + (\boldsymbol{\mu_y} - \boldsymbol{\mu_x})^{\text{T}}\boldsymbol{\Sigma_y^{-1}}(\boldsymbol{\mu_y} - \boldsymbol{\mu_x})\right]$$

所以能够计算KL散度。不过有更简单的方法，并不需要实际计算出KL散度。如何去简单地 minimize 一个这样的KL散度呢？

再次回顾一下，这两个高斯分布的本质。

$q(x_{t-1} | x_t, x_0)$ 是高维空间中的多元高斯分布，通过计算，mean 和方差是固定的，与神经网络无关。

$P_\theta(x_{t-1}|x_t)$ 才是由神经网络决定的。$P(x_{t-1}|x_t)$ 是 逆过程（reverse process）分布，我们通过训练神经网络 $P_\theta(x_{t-1}|x_t)$ 来近似它。我们不讨论高斯分布 $P_\theta(x_{t-1}|x_t)$ 的方差，假设它是定值，这是因为方差对性能影响不大，而且加入预测方差的功能会增加训练复杂度。

我们只考虑它的mean。

那么， minimize 这样两个高斯分布的KL散度的方法就显而易见了：

如图，把右边的 mean 往左边移移，靠近一下左边的 mean，KL散度不就变小了吗？

让我们关注一下minimize的过程吧，如图，

上图是先 sample 一个 $x_0$ ，通过之前的推导，得出 $x_t$。接下来，我的 denoise model 要做的是，输入 t 与 $x_t$ ，产生输出。

输出的结果，就是 $P_\theta(x_{t-1}|x_t)$的 mean，它要与 $q(x_{t-1} | x_t, x_0)$ 的mean，即

$$\tilde{\mu}_t(x_t, x_0) = \frac{\sqrt{\bar{\alpha}_{t-1}} \beta_t}{1 - \bar{\alpha}_t} x_0 + \frac{\sqrt{1 - \beta_t} (1 - \bar{\alpha}_{t-1})}{1 - \bar{\alpha}_t} x_t$$

越接近越好。如图，就是上述过程：

其中还可以再变形，我们做些移项和变换，有

$$x_t = \sqrt{\bar{\alpha}_t}x_0 + \sqrt{1 - \bar{\alpha}_t}\varepsilon \\$$ $$x_t - \sqrt{1 - \bar{\alpha}_t}\varepsilon = \sqrt{\bar{\alpha}_t}x_0 \\$$ $$\frac{x_t - \sqrt{1 - \bar{\alpha}_t}\varepsilon}{\sqrt{\bar{\alpha}_t}} = x_0$$

把它带入 $q(x_{t-1} | x_t, x_0)$ 的mean，有

$$\tilde{\mu}_t(x_t, x_0) \\$$ $$= \frac{\sqrt{\bar{\alpha}_{t-1}} \beta_t}{1 - \bar{\alpha}_t} x_0 + \frac{\sqrt{1 - \beta_t} (1 - \bar{\alpha}_{t-1})}{1 - \bar{\alpha}_t} x_t \\$$ $$= \frac{\sqrt{\bar{\alpha}_{t-1}}\beta_t \left(\frac{x_t - \sqrt{1 - \bar{\alpha}_t}\varepsilon}{\sqrt{\bar{\alpha}_t}}\right) + \sqrt{\bar{\alpha}_t}(1-\bar{\alpha}_{t-1})x_t}{1 - \bar{\alpha}_t} \\$$ $$= \frac{1}{\sqrt{\bar{\alpha}_t}} \left(x_t - \frac{1-\alpha_t}{\sqrt{1-\bar{\alpha}_t}}\varepsilon\right)$$

这就是我们训练denoise model要输出的目标。

其中，$\alpha$ 都是设定好的，$x_t$ 是输入，因此denoise model神经网络需要预测的就是 $\epsilon$ 。而denoise model的输出就是

$$\frac{1}{\sqrt{\bar{\alpha}_t}} \left(x_t - \frac{1-\alpha_t}{\sqrt{1-\bar{\alpha}_t}}\varepsilon\right)$$

我们回到算法的伪代码部分，这下清晰明了了，

Algorithm 2: Sampling

1. $x_T \sim \mathcal{N}(0, \mathbf{I})$
2. for $t = T, \dots, 1$ do
3.     Sample $z \sim \mathcal{N}(0, \mathbf{I})$ if $t > 1$, else $z = 0$
4.     Compute:

$$x_{t-1}=\frac{1}{\sqrt{\alpha_t}} \left( x_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \epsilon_\theta(x_t, t) \right) + \sigma_tz$$

1. end for
2. return $x_0$

$\sigma_tz$ 的解释

最后要解决的问题是：为什么要加一个$\sigma_tz$？

我们的denoise model的输出就是一个高斯distribution，那 $x_{t-1}$ 这个样本的取样，为什么不直接取这个高斯分布的mean，而是要加上$\sigma_tz$呢？

类似的问题在 NLP 领域也有，比如

这个随机性为什么是需要的？对于 GPT，如果每次取最大的概率，会反复重复一句话。人们对此的分析是，人写的句子遣词造句不是选择几率最大的词汇，如果将人类文章每个词的概率算出来，会是时大时小的，

语音合成也是同理，为了避免某些神经元“一步到位”，要对神经元 dropout。

denoise model 防止“一步到位”的方法，就是加上从高斯分布中取样的 noise。

以上就是 Diffusion Model 的原理。

Diffusion Model 应用

这里就简单介绍一下，例如，语音合成：

放在文字处理上似乎有点困难，因为文字是独立的，不能视为高斯分布的某个取样。但是它可以用在词嵌入上，

也可以将高斯分布换为文字能使用的distribution，

Diffusion Model 中，“‘一步到位’改为‘ N 步到位’”的思想也广泛应用。例如用来解决 GPT 等 Autoregressive Model 会“举棋不定”的问题。